we have a vertical parabola (quadratic equation) open upward
we know that
The y-intercept is the value of y when the value of x is equal to zero
In this problem
looking at the graph
the y-intercept is the point (0,2)
so
(0,2) is a solution
The vertex of the function is the point (1,1)
Determine the equation of the quadratic equation in vertex form
The equation is equal to
y=a(x-h)^2+k
where
a is a coefficient
(h,k) is the vertex
we have
(h,k)=(1,1)
substitute
y=a(x-1)^2+1
Find the value of a
we have the y-intercept (0,2)
substitute in the equation and solve for a
2=a(0-1)^2+1
2=a+1
a=1
therefore
teh equation is
y=(x-1)^2+1
Determine the x-intercepts
Remember that the x-intercepts are the values of x when the value of y is equal to zero
In this problem the x-intercepts are complex number
so
For y=0
(x-1)^2+1=0
(x-1)^2=-1
take square root both sides
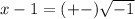
Remember that
i^2=-1
so
x-1=(+/-)i
x=(+/-)i+1
therefore
the x-intercepts are
(i+1,0) and (-1+1,0)
therefore
the answer for this problem is option C