EXPLANATION
We are told that the payoff for the raffle is one million dollars and we know that each ticket has the following chances of being a winner:
1:125,000
The probability is given by the following relationship:

We need to use the expected means formula and substitute the x variable for the given payoff for the lottery ticket.

Replacing terms:

Simplifying:
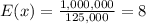
The expected payoff is 8 dollars. If