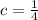A quadratic's general form is:
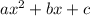
Our trinomial given is:
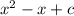
From matching it with the general form, we can say that:
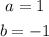
For this to be a perfect square trinomial, c will take the value:
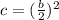
We know b = -1, thus c will be:
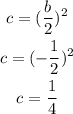
Thus, the value of c that will make this a perfect square trinomial: