Question

What is the sum of the first 14 terms of the series?

Answer 1

The sum of n terms of AP is the sum(addition) of the first n terms of the arithmetic sequence.

It is equal to n divided by 2 times the sum of twice the first term – ‘a’ and the product of the difference between second and first term - ‘d’ also known as common difference, and (n-1), where n is the number of terms to be added.

The formula is given to be:

`S=(n)/(2)(2a+\lbrack n-1\rbrack d)`

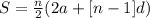
From the series given, we have the following parameters:

`\begin{gathered} a=12 \\ d=4-12=-8 \\ n=14 \end{gathered}`

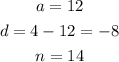
Substituting these values into the formula, we have:

`\begin{gathered} S_(14)=(14)/(2)(2*12+\lbrack14-1\rbrack*-8) \\ S_(14)=7(24+\lbrack13*-8\rbrack) \\ S_(14)=7(24-104) \\ S_(14)=7*-80 \\ S_(14)=-560 \end{gathered}`

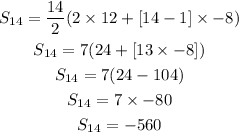
The sum of the first 14 terms is -560.

The correct option is the THIRD OPTION.