Given:
The mass of the truck, m=5000 kg
The initial speed of the truck, u=25 m/s
The final speed of the truck, v=0 m/s
The time it takes for the truck to come to a stop, t=8 s
To find:
The braking force needed to bring the truck to a stop.
Step-by-step explanation:
The acceleration of an object is the time rate of change of the velocity of the object.
Thus the acceleration of the truck is given by,
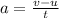
From Newton's second law of motion, the force needed to bring the truck to a stop is given by,

On substituting the known values,
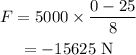
The negative sign indicates that the force is applied in the direction opposite to the direction of motion of the truck.
Final answer:
Thus the braking force needed to bring the truck to a stop is 15625 N