Question

5 in3 inThe volume ofthe figure iscubic in.6 in3 in3 in7 in16 in.

Answer 1

So we need to find the volume of a figure composed of another two subfigures: a red one and a green one.

The green subfigure is composed of six rectangular faces and all the angles between its sides are right angles. This means that its colume is given by the product between the area of one of its faces and the length of the sides that are perpendicular to that face. For example, the area of the bottom face is given by:

`16in\cdot7in=112in^2`

So its area is 112in². The length of its perpendicular sides is 3 inches so the volume of the green figure is equal to:

`112in^2\cdot3in=336in^3`

So we have found the volume of the first subfigure, we still need to find that of the red subfigure. This one is a prism with a pair of triangular faces that we are going to call its bases. The volume of this prism is equal to the area of one of this bases multiplied by the length of the sides that are perpendicular to it. The area of a triangle is equal to the product of its base and its height divided by 2. The base of the triangular face is 3 inches long whereas its height is 5 inches long. Then the area of the triangular face is:

`(5in\cdot3in)/(2)=(15)/(2)in^2=7.5in^2`

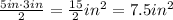
Then the volume of the red subfigure is:

`7.5in^2\cdot6in=45in^3`

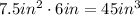
Finally, the volume of the entire figure is the sum of the volumes of the subfigures:

`V=336in^3+45in^3=381in^3`

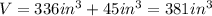
Then the answer is 381.