The cone has a height of h = 4.5 in and a diameter of d = 2 in.
The radius is r = d/2 = 1 in.
The volume of a cone is:
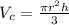
Substituting:

We assume each scoop of ice cream is a semisphere of diameter d = 3 in, or radius r = 1.5 in.
The volume of each scoop is:
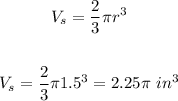
The Single size has one scoop of ice cream, thus the total volume is:
1.5π + 2.25π = 3.75π cubic inches = 11.781 cubic inches.
This size costs $3.50. The unit cost is:
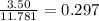
It costs approximately $0.30 per cubic inch of ice cream.
The Double size has two scoops of ice cream, thus the total volume is:
1.5π + 2 x 2.25π = 6π cubic inches = 18.850 cubic inches.
This size costs $4.50. The unit cost is:
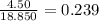
It costs approximately $0.24 per cubic inch of ice cream.
The Triple size has three scoops of ice cream, thus the total volume is:
1.5π + 3 x 2.25π = 8.25π cubic inches = 25.918 cubic inches.
This size costs $5.50. The unit cost is:

It costs approximately $0.212 per cubic inch of ice cream.
This last size has the least price per volume of ice cream, so it's better for the customers.
The table is shown below.