Question

Hello, could you help me with this problem, I am not sure how to do it. Thank you

Answer 1

Answer: Yes the diagonals are perpendicular

==========================================================

Step-by-step explanation:

The diagonals connect the non-adjacent vertices.

The two diagonals in this case are CE and DF.

-----------------------

Let's use the slope formula to compute the slope of segment CE.

C = (0,0)

E = (9,6)

`(x_1,y_1) = (0,0) \text{ and } (x_2,y_2) = (9,6)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (6 - 0)/(9 - 0)\\\\m = (6)/(9)\\\\m = (2)/(3)\\\\`

Segment CE has a slope of 2/3.

----------------------

Now we'll find the slope of diagonal DF.

D = (8,1)

F = (4,7)

`(x_1,y_1) = (8,1) \text{ and } (x_2,y_2) = (4,7)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (7 - 1)/(4 - 8)\\\\m = (6)/(-4)\\\\m = -(3)/(2)\\\\`

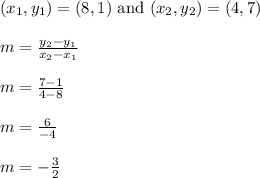
Segment DF has slope -3/2.

----------------------

Summary:

• Diagonal CE has slope 2/3
• Diagonal DF has slope -3/2

The product of those slopes is (2/3)*(-3/2) = -6/6 = -1

The slopes having a product of -1 is sufficient evidence to show the diagonals being perpendicular. The two diagonals meet up to form a 90 degree angle. This property is true of any kite in geometry.

Notice how -3/2 is the negative reciprocal of 2/3, and vice versa.