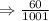Step-by-step explanation:
The number of black balls is
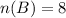
The number of red balls in the urn is
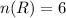
The total number of balls will be calculated as
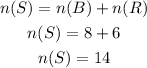
Step 1:
Get the numerator
To do this, we will have to choose one black from the 8 black balls below as
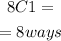
We will now choose the reamining balls from the 6 red balls which will give us
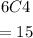
Hence,
The numerator will be
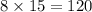
Step 2:
We will get the deonminator below as
Choosing 5 balls from 14
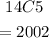
Therefore,
the probability og picking exactly one ball will be
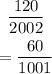
Hence,
The Probability that exactly 1 black ball is drawn will be