the average body mass index (BMI) in the 25 to 39 age group for women was found to be 24 with a standard deviation of 5
From the above, we can obtain this information:
mean: μ = 24
standard deviation: σ = 5
Question
a woman from this age group is selected at random, what is the probability she has a BMI between 32 and 35.
P ( 32
In order to find P ( 32
First, we need to calculate z-value
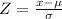
P(x<35)
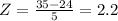
now, we can use a Z-score table to find the probability having the above z-value of 2.2
P(z<2.2) = 0.9861
Therefore, P(x<35) = 0.9861
P(x<32)
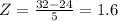
Again, using the Z-score table, for a value of Z=1.6, the probability is
P(z<1.6) = 0.9452
Therefore, P(x<32) = 0.9452
Finally, we must solve P(x<35) - P(x<25) to find P(32this is: 0.9861 - 0.9452 = 0.0409
Which is the same as: P(1.6or P(32
In conclusion, the probability of selecting a woman with an IBM between 32 and 35 is P = 0.0409