A line is said to be flat when it has a small slope, while a line is said to be steep when it has a large slope.
Let's find the slope of both lines.
Apply the slope formula:

• Slope of line A
Take the points:
(x1, y1) ==> (-1, 1)
(x2, y2) ==> (-2, 4)

• Slope of line B
Take the points:
(x1, y1) ==> (4, -1)
(x2, y2) ==> (0, -1)
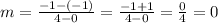
The slope of line A is -3( negative slope)
The slope of line B is 0
The greater the slope, the steeper the line.
• Since line B has a greater slope than line A, we can say it is steeper.
,
• Also since Line B is a horizontal line, it is flatter than line A
,
• The slope of a horizontal line is greater than the slope of a line with a neagtive slope, we can say that line B shifted upward
Thus, we can say:
Line B is flatter, horizontal and shifted upward
ANSWER:
Line B is flatter, horizontal, and shifted upward