Question

a) Find the common velocity of the trucks after collision b) find the magnitude of the impulse experienced by the heavier truck during the collision c)Determine whether the collision is elastic or inelastic

Answer 1

a)

In order to calculate the common velocity after the collision, we can use the equation of the conservation of momentum:

`m_1v_(1i)+m_2v_(2i)=m_1v_(1f)+m_2v_(2f)`

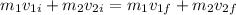
So, using m1 = 5000, m2 = 3000, v1i = 3.2, v2i = 2.4 and v1f = v2f = v, we have:

`\begin{gathered} 5000\cdot3.2+3000\cdot2.4=5000v+3000v\\ \\ 8000v=16000+7200\\ \\ 8000v=23200\\ \\ v=2.9\text{ m/s} \end{gathered}`

b)

To find the impulse, we can calculate the change in momentum of the truck (Impulse theorem):

`\begin{gathered} I=\Delta p=p_f-p_i\\ \\ I=m_1(v_-v_(1i))\\ \\ I=5000\cdot(2.9-3.2)\\ \\ I=5000\cdot(-0.3)\\ \\ I=-1500\text{ Ns} \end{gathered}`

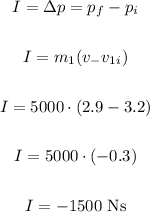
c)

There are two main differences between an elastic and an inelastic collision.

Elastic:

- The total kinetic energy of the system is maintained.

- The masses don't move together after the collision.

Inelastic:

- The total kinetic energy of the system is not maintained.

- The masses move together after the collision.

Since the two masses moved together after the collision, we have an inelastic collision.