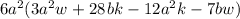Question

18a4w + 168a²bk – 72a4k – 42a²bw

Answer 1

Factoring the expression with the GCF will give;

`6a^2(3a^2w^{}+28^{}bk^{}-12a^2k^{}-7bw^{})^{}`

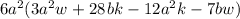
Step-by-step explanation:

Given the expression;

`18a^4w+168a^2bk-72a^4k-42a^2bw`

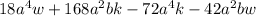
Let us find the greatest common factor of the expressions;

`\begin{gathered} 18a^4w+168a^2bk-72a^4k-42a^2bw \\ 18a^4w=2*3*3* a* a* a* a* w \\ 168a^2bk=2*2*2*3*7* a* a* b* k \\ -72a^4k=-1*2*2*2*3*3* a* a* a* a* k \\ -42a^2bw=-1*2*3*7* a* a* b* w \\ \text{GCF}=2*3* a* a=6a^2 \end{gathered}`

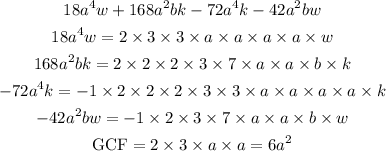
Therefore, the greatest common factor of the expressions is;

`6a^2`

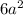
Factoring the expression;

`\begin{gathered} 18a^4w+168a^2bk-72a^4k-42a^2bw \\ =6a^2((18a^4w+168a^2bk-72a^4k-42a^2bw))/(6a^2) \\ =6a^2((18a^4w)/(6a^2)+(168a^2bk)/(6a^2)-(72a^4k)/(6a^2)-(42a^2bw)/(6a^2))^{} \\ =6a^2(3a^2w^{}+28^{}bk^{}-12a^2k^{}-7bw^{})^{} \end{gathered}`

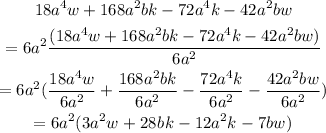
Therefore, factoring the expression with the GCF will give;

`6a^2(3a^2w^{}+28^{}bk^{}-12a^2k^{}-7bw^{})^{}`