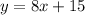
Step-by-step explanation
Step 1
2 lines are parallel if they have the same slope, so
a) let's check the slope of the given line
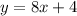
it is in the form
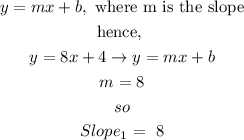
so, the slope of the line we are looking for is 8
Step 2
Now, to find the equation of the line, we can use this expression

then, Let

replace,
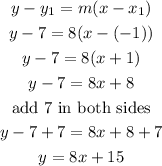
therefore, the answer is
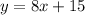
I hope this helps you