Question

Two vertices of the triangle in the figure represent therelative positions of boats on opposite sides of alighthouse. The angles of elevation from the boats tothe top of the lighthouse are x° and yº.8=1517=>sin(x) cos(xº) = tan(°) =• sin(yº) = f, cos(yº) = }, tan(yº) = jLighthouseܘܐBoatBoatCreate a fraction to represent the ratio of the heightof the lighthouse to the distance between the boats.111:: 3:: 4:: 5:: 8:: 15:: 17:: 18:: 21:: 22

Answer 1

Take into account that the distances between the boats and the height of the lighthouse form right triangles.

Then, you have for the tangent of angles x and y, the following expressions:

`\begin{gathered} \tan (x)=\frac{height\text{ of the lighthouse}}{\text{distance from boat A to light house}} \\ \tan (y)=\frac{height\text{ of the lighthouse}}{\text{distance from boat B to light house}} \end{gathered}`

you can notice on the given information that tan(y) = 4/3, then, the fraction between th height of the light house and the distance from boat B is 4/3.

For the other fraction (height of lighthouse over the distance from boat A) consider that

`\tan (x)=(\sin (x))/(\cos (x))=((8)/(17))/((15)/(17))=(8)/(15)`

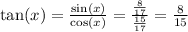
Hence, the fraction between the heoght of the lighthouse and the distance from boat A is 8/15