Question

i need help with this asapcalculation a is (ACCURATE/INACCURATE) because it (incorrectly factors of numerator/use a synthetic division which is not appropriate for this situation/factors of numerior and reveals the denominator is a factor/factors that denominator not the numerator/is a simplified form of one of the factors of the numerator)calculation B is (accurate/inaccurate) because it (factors the numerator and reveals of denominator is a factor/is a simplified form of one of the factors of the numerator/use the synthetic division which is not appropriate for the situation/factors of denominator not the Numerator/incorrectly factors denominator the numerator

Answer 1

We are given the following rational expression:

`(x^4-4x^3-6x^2+20x-75)/(x^2-2x+5)`

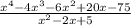
For calculation A we notice that when performing an algebraic division the result was:

`x^2-2x-15`

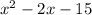
And the remainder was zero. This means that the numerator can be factored as:

`x^4-4x^3-6x^2+20x-75=(x^2-2x+5)(x^2-2x-15)`

Therefore, calculation A is accurate because it factors the numerator and reveals that the denominator is a factor.

In the case of calculation B we notice that there is an error in the second part of the division. When "2x" was multiplied by the dividend the result is:

`2x(x^2-2x+5)=2x^3-4x^2+10x`

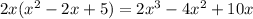
But in the operation the result was:

`2x^3-4x^2-10x`

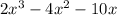
Therefore, Calculation B is inaccurate, because it incorrectly factors the numerator.