Solve the system of equations by substitution;
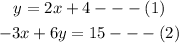
From equation (1), we note that y equals 2x plus 4, hence we substitute this value of y into equation (2)
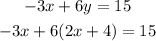
Next, we expand the parenthesis on the left side of the equation
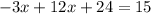
Next we collect all like terms as follows;
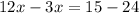
Solve this and we arrive at;
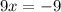
Divide both sides by 9
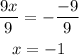
We can now substitute for x = -1 into equation (1)
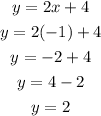
The solution is
x = -1, y= 2