We are given that the cost to send a package is $8 and that the cost increases by $4 for each integer pound after 1.
First, we muse defined the greatest integer function. This function assigns the greatest integer that is smaller that the argument of the function and its symbol is:

For example, if x = 0.5, the greatest integera that is smaller than 0.5 is 0, therefore:

Is "x = 1.5" we have:
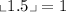
Now, to determine a cost function we need to add to the $8 a charge of $4 each time that the weight "w" reaches a new integer, therefore, the function is:
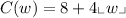
Now, if we plug in the value of "w = 0.5" we get:
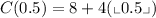
Now, we solve the operations:
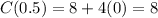
Now, if "w = 1", we get:
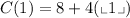
Solving the operation:
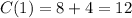
If "w = 1.5" we get:
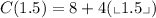
Solving the operation we get:
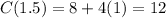
The same procedure is used for the other values of the table.
A graph of the data must look like this:
The graph presents constant lines until the value of "x" reaches a new decimal number where the graph jumps to a new constant line.
A piecewise function would be a function that does not make use of the greatest integer function.
To construct is we need to have into account each of the constant values of the function and the interval associated with each of the values. For the constant value of "C(w) = 8" we have the interval:
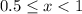
For the constant value of 12 we have the interval:
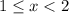
And, for the constant value of 16 we have the interval:
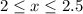
Therefore, we write the piecewise function as:
