Question

a rectangle has a diagonal 20 inches long that forms angles of 60 degrees and 30 degrees with a sides. find the perimeter of the rectangle.

Answer 1

Given:

The length of the diagonal of a rectangle is 20 inches.

The angles formed by the diagonal are 60° and 30°.

The objective is to find the perimeter of the rectangle.

The rectangle can be represented as,

In general, the angle formed by two larger sides will be smaller and the angle formed by two smaller sides will be larger.

Consider the right triangle ABC. AC represents the hypotenuse side, AB represents the adjacent side and BC represents the opposite side of the triangle.

Now, the side BC can be calculated using trigonometric ratio of sinθ.

`\begin{gathered} \sin \theta=\frac{opposite}{\text{hypotenuse}} \\ \text{sin}30\degree=(BC)/(AC) \\ (1)/(2)=(BC)/(20) \\ BC=(20)/(2) \\ BC=10\text{ inches.} \end{gathered}`

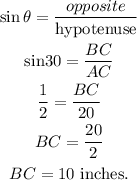
Now, the side AC can be calculated using trigonometric ratio of cosθ.

`\begin{gathered} \cos \theta=\frac{adjacent}{\text{hypotenuse}} \\ \cos 30\degree=(AB)/(20) \\ \frac{\sqrt[]{3}}{2}=(AB)/(20) \\ AB=20\cdot\frac{\sqrt[]{3}}{2} \\ AB=10\sqrt[]{3} \\ AB=17.32 \end{gathered}`

In a triangle the opposite sides are always equal.

`\begin{gathered} AB=CD \\ BC=AD \end{gathered}`

The perimeter of the rectangle is,

`\begin{gathered} P=AB+BC+CD+AD \\ =17.32+10+17.32+10 \\ =54.64\text{ inches} \end{gathered}`

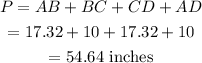
Hence, the perimeter of the rectangle is 54.64 inches.