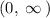Question

Please help me all the tutor can’t answer my question if you can’t answer don’t accept

Answer 1

Let's determine the compund functions, firts.

1) already solved.

2) h(m(x)):

`h(m(x))=h(x^2-4)=\frac{1}{\sqrt[]{(x^2-4)^{}}}`

3) m(h(x)):

`m(h(x))=m(\frac{1}{\sqrt[]{x}})=(\frac{1}{\sqrt[]{x}})^2-4`

Let's work with equation 2. We need to simplify it.

`\begin{gathered} \frac{1}{\sqrt[]{(x^2-4)^{}}}\cdot(√(x^2-4))/(√(x^2-4)) \\ =(1\cdot√(x^2-4))/(√(x^2-4)√(x^2-4)) \\ =(√(x^2-4))/(x^2-4) \end{gathered}`

Now, let's stablish the conditions to find its domain:

Cond. 1)

`x^2-4\\e0`

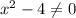
Cond. 2)

`x^2-4>0`

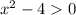
condition 2 implicitly includes condition 1, then we will work from it

`\begin{gathered} x^2-4>0 \\ x^2-4+4>0+4 \\ x^2>4 \\ x<-√(4)\quad \mathrm{or}\quad \: x>√(4) \\ x<-2\quad \mathrm{or}\quad \: x>2 \end{gathered}`

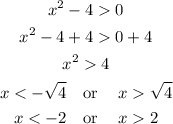
in interval notation:

`\mleft(-\infty\: ,\: -2\mright)\cup\mleft(2,\: \infty\: \mright)`

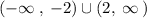
Now, let's work with the 3rd compound function

`(\frac{1}{\sqrt[]{x}})^2-4`

In this case, x must be greater than and different from zero. Therefore, the domain will be:

`x>0`

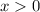
in interval notation:

`\mleft(0,\: \infty\: \mright)`