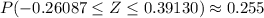Question

The monthly utility bills in a city are normally distributed with a mean of $121 and a standard deviation of $23. Find the probability that a randomly selected utility bill is between $115 and $130.0.2550.4520.6030.397

Answer 1

Given a normal random distribution with mean μ and standard deviation σ:

`\begin{gathered} \mu=121 \\ \sigma=23 \end{gathered}`

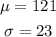
The z-score can be calculated using the formula:

`Z=(X-\mu)/(\sigma)`

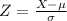
Where X is a value of the normal random distribution. We need the probability that a randomly selected utility bill is between $115 and $130. The z-scores of these values are:

`\begin{gathered} Z_1=(115-121)/(23)=-(6)/(23)\approx-0.26087 \\ Z_2=(130-121)/(23)=(9)/(23)\approx0.39130 \end{gathered}`

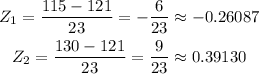
Then, we need to calculate the probability of:

`P(Z_1\leq Z\leq Z_2)=P(-0.26087\leq Z\leq0.39130)`

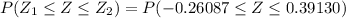
Using the tables of the z-distribution, this probability is:

`P(-0.26087\leq Z\leq0.39130)\approx0.255`