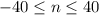1 Answer

Lukeshek · Answer 1 · 2023-07-17T04:23:46+0000

Given the Absolute Value Inequality:

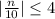
$|(n)/(10)|\leq4$

You can solve it as follows:

1. Split the inequality into two inequalities:

- Inequality 1:

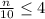
$(n)/(10)\leq4$

- Inequality 2:

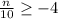
$(n)/(10)\ge-4$

2. Solve for "n" on each inequality:

- Inequality 1:

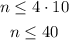
$\begin{gathered} n\leq4\cdot10 \\ n\leq40 \end{gathered}$

- Inequality 2:

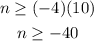
$\begin{gathered} n\ge(-4)(10) \\ n\ge-40 \end{gathered}$

3. You can write the solution as follows:

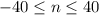
$-40\leq n\leq40$

Hence, the answer is:

$-40\leq n\leq40$

Please log in or register to add a comment.