SOLUTION
The points are
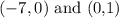
The equation is writing using the formula below
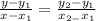
where
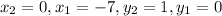
Then, we substitute the parameters into the formula above
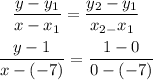
Simplifying further, we have
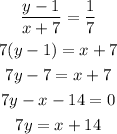
Then in the slope-intercept form, we have the equation as
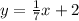
Therefore the equation of the line in the slope-intercept form is
y=(1/7)x +2