Question

You have been given 2.431 g of copper from which you are to fashion a wire whose resistance is 1,096.259 ohms. The density of copper is 8900 kg/m 3 and the resistivity of copper is 1.7 x 10 -8 ohm m. What will the diameter, in mm, of the wire be that you fashion?

Answer 1

This question is for us to apply Ohm's second law. This law tells us the following:

`R=(\rho.L)/(A)`

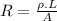
But first, for us to find the diameter and area, we need to know how much (in volume) of copper we have. This can be achieved by using the information of copper density and mass. We know that

`m=d_v*v`

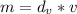
Where m is the mass, dv is the density and v is the volume. By replacing our values we get:

`2.431*10^(-3)=8900*v`

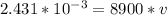
Thus, our volume is

`v=(m)/(d_v)=(2.431*10^(-3))/(8900)=2.7315*10^(-7)m^3`

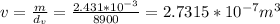
After finding the volume, we can return to Ohm's second law. Replacing our information we get

`1096.259=(1.7*10^(-8)*L)/(A)`

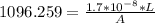
But we also know our volume, then

`L*A=2.7315*10^(-7)m^3`

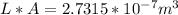
Then we have two equations and two variables. This system can be solved. If we rearrange the second equation we get

`L=(2.7315*10^(-7))/(A)`

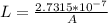
And replacing it on the first equation

`1096.259=(1.7*10^(-8))/(A)*(2.7315*10^(-7))/(A)=(4.64355*10^(-15))/(A^2)`

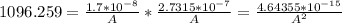
Rearranging, we get

`A^2=(4.64355*10^(-15))/(1096.259)=4.2358*10^(-18)`

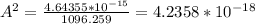
Finally, we can find the area with this equation, which yields

`A=\sqrt[2]{4.2358*10^(-18)}=2.058*10^(-9)m^2`

However, we're not done yet. Our conductor will be a cylinder, and we want to find its radius. Then, we know our area is

`A=\pi r^2`

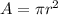
Thus

`r=\sqrt[2]{(A)/(\pi)}`

Plugging in the information we found out about the area, we get

`r=\sqrt[2]{(2.058*10^(-9))/(\pi)}=2.559*10^(-5)m`

Our final answer then is r=0.02559mm