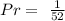SOLUTION:
Case: A deck of cards (Probability)
A standard deck of cards has four suites: hearts, clubs, spades, diamonds. Each suite has thirteen cards: ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen and king. There are 52 cards in the deck.
Given:
A case of replacement. Picking a 9 on the first draw and a diamond on the second draw
Required: To find the probability of picking a 9 on the first draw and a diamond on the second draw
Method:
Total number of cards: 52
Number of 9's = 4 (From the four different suites)
Number of diamonds= 13 (From each suites)

Final answer:
The probability of taking a 9 and then a diamond with replacement is: