Question

38. DRAWING CONCLUSIONS You deposit S2200 into three separate bank accounts that each pay 3% annual interest. How much interest does each account earn after 6 years?

Answer 1

Account 1 $432.08

Account 2 $433.29

Account 3 $433.85

Step-by-step explanation

For Account 1

P = $2200

r = 3%

n = 6 years

Since the acoount is compounding quarterly, this implies

r = 3/4 % = 0.75% = 0.0075

A = ?

Using the compound interest formula

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ A=2200(1+0.0075)^(6*4) \\ A=2200(1.0075)^(24) \\ A=2200(1.1964) \\ A=2632.08 \end{gathered}`

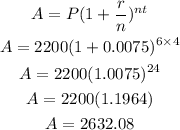
Therefore, the interest on Account 1 after 6 years = A - P

Interest = $2632.08 - $2200 = $432.08

For Account 2

Since the acoount is compounding monthly, this implies

r = 3/12 % = 0.25% = 0.0025

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ A=2200(1+0.0025)^(6*12) \\ A=2200(1.0025)^(72) \\ A=2633.29 \\ \end{gathered}`

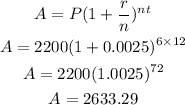
Therefore, the interest on Account 2 after 6 years = A - P

Interest = $2633.29 - $2200 = $433.29

For Account 3

Since the acoount is compounding daily, this implies

r = 3/365 % = 0.008219% = 0.00008219

`\begin{gathered} A=2200(1+0.00008219)^(6*365) \\ A=2200(1+0.00008219)^(2190) \\ A=2633.85 \end{gathered}`

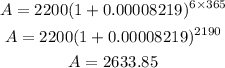
Therefore, the interest on Account 3 after 6 years = A - P

Interest = $2633.85 - $2200 = $433.85