First we need to find the mean and the standadr deviation. For the mean, we sum the values up and divide by the number of data given. We have 8 data, so:
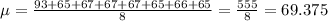
Now, we need the standard deviation. To find it, we use the formula:
![\sigma=\sqrt[]{\frac{\sum ^{}_{}(x_i-\mu)^2}{N-1}}](https://img.qammunity.org/2023/formulas/mathematics/college/wjt6lcbe0p269skz2e4ofe177wp7qib5t0.png)
The sum symbol in there mean we need to get each data given, substract the mean we calculated, square them and then sum all. N is the number of data, which is 8. Let look one example:
For data 93, we do:
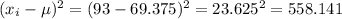
Now, we do the same for the others:
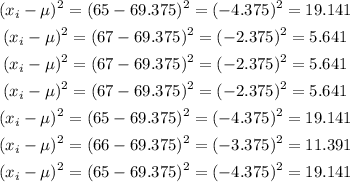
Now we sum all of them:
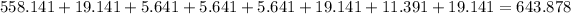
This goes into the formula.
![\sigma=\sqrt[]{(643.878)/(8-1)}=\sqrt[]{(643.878)/(7)}=\sqrt[]{91.982}=9.591](https://img.qammunity.org/2023/formulas/mathematics/college/umgtyxx4fea7jhpqocg3fggglms1bw050n.png)
Now, we want the number of data that is within 2 standard deviation from the mean. Thus, we want the data that are between:
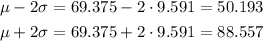
From the given Data, 93 is out of this range, but all the others (65, 67, 67, 67, 65, 66, 65) are in it. So, the number of data within 2 standard deviations from the mean is 7.