Question

Mike is about to take a history test consisting of matching questions worth 10 points each and essay questions worth 30 points each. He is required todo at least 4 matching questions, but time restricts doing more than 10. Similarly, he must do at least 4 essays, but time restricts doing more than 12. If Mike can answer no more than 20 questions, how many of each type should he answer to maximize his score? What is the maximum score?

Answer 1

Given that matching questions are worth 10 points each, and essay questions are worth 30 points each.

Let the number of matching questions done be x, and the number of essay questions be y.

Mike is required to do at least 4 but time resricts doing more than 10. This implies that

`4\leqslant x\leqslant10`

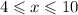
Similarly, he must do at least 4 essays, but time restricts doing more than 12. This implies that

`4\leqslant y\leqslant12`

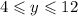
If Mike can answer no more than 20 questions, this implies that

`x+y\le20`

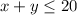
Mike can either answer

`4\text{ matchi}ng\text{ questions and 12 essay questions}`

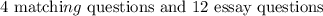
or

`10\text{ matchi}ng\text{ questions and 4 essay questions}`

The number of each type to maximize his score:

For Matching questions: Mike answers 4 questions.

For Essay questions: Mike answers 12 essay questions

Maximum score:

Recall that a matching question is worth 10 points each, and an essay question is worth 30 points each. Thus, the maximum score is evaluated as

`\begin{gathered} 10(4)\text{ +30(12)} \\ =40+360 \\ =400\text{ points} \end{gathered}`

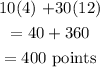
Hence, his maximum point is 400 points.