Question

The position from its starting point of a small plane preparing for takeoff is given by…

Answer 1

Data:

• Position equation

`x(t)=1.9t^2`

The exercise is asking for speed.

The first derivative of position is speed.

Procedure:

1. Calculating the first derivative: obtaining the equation of speed v ( t )

`\begin{gathered} v(t)=(dx)/(dt) \\ v(t)=1.9\cdot2t \\ v(t)=3.8t \end{gathered}`

2. Calculating the time it takes to reach 45.6m/s: isolating t

`\begin{gathered} v(t)=3.8t \\ t=(v(t))/(3.8) \\ t=(45.6)/(3.8) \\ t=12 \end{gathered}`

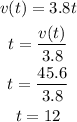
Answer: 12s

Summary:

0. Calculating the first derivative of position, which equals to speed

,

1. Isolating ,t

,

2. Obtaining the time