Question

Calculate the gravitational force of the sun on mars if the distance between these two celestial bodies is approximately 143.82 million miles (assume this measurement is center to center). The given mass of the sun is 1.99 x 10^30 kg, the given mass of mars is 6.42 x 10^23 kg. The given radius of the sun is 6.96 x 10^8 m, the given radius of mars is 3.40 x 10^6 m.

Answer 1

Given:

The distance between the sun and mars is

`\begin{gathered} d=143.82\text{ million miles} \\ =143.82*10^6\text{ miles} \end{gathered}`

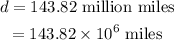
The sun has mass

`m_s=1.99*10^(30)\text{ kg}`

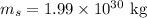
The mass of mars is

`m_m=6.42*10^(23)\text{ kg}`

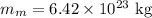
To find:

The gravitational force of the sun on mars

Step-by-step explanation:

The gravitational force between two objects is,

`\begin{gathered} F=(Gm_1m_2)/(d^2) \\ G=6.67*10^(-11)\text{ N.m}^2.kg^(-2) \end{gathered}`

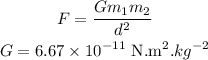
The distance between the sun and mars is, (the distance here is between the centres of the celestial bodies so we need not add the radii here)

`d=143.82*10^6*1609.34\text{ m}`

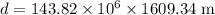
Substituting the values we get,

`\begin{gathered} F=(6.67*10^(-11)*1.99*10^(30)*6.42*10^(23))/((143.82*10^6*1609.34)^2) \\ =1.59*10^(21)\text{ N} \end{gathered}`

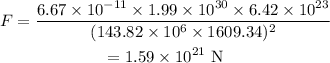
Hence, the gravitational force is

`1.59*10^(21)\text{ N}`