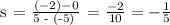The first thing is to calculate the slopes of the mentioned lines:
The slope has te following formula:
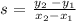
A. The slope of (f) is - 1/5
Cordinates of f:
(-5, 3) and (5, 1)
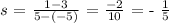
A is true
B. The slope of (d) is - 1/5
Cordinates of d:
(-5, -1) and (5, -4)
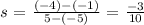
B is false
C. The slope of (a) is 5/2
Cordinates of a:
(-5, -5) and (-1, 5)
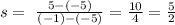
C is true
D. The slope of (b) is - 5/2
Cordinates of b:
(-3.5, -5) and (0.5, 5)
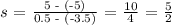
D is false
thefore only A and C are true
The slope de (c):
Cordinates of c:
(0, -5) and (4, 5)
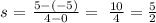
The slope de (e):
Cordinates of e:
(-5, 0) and (5, -2)