Question

Solve 1/2r^2-10= 3/2r2 using square roots. Select the solution(s).POSSIBLE SOLUTIONSA) r=(radical symbol here) -10B) r= -(radical symbol here) -10C) r= -(radical symbol here) 5D) r= (radical symbol here) 5E) no real solution

Answer 1

There is no real solution

The solutions are imaginary, and they are:

`r=\sqrt[]{-10}`

and

`r=-\sqrt[]{-10}`

Step-by-step explanation:

Given the equation:

`(1)/(2)r^2-10=(3)/(2)r^2`

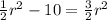
To solve this, first subtract

`(1)/(2)r^2`

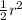
from both sides of the equation

`\begin{gathered} (1)/(2)r^2-10-(1)/(2)r^2=(3)/(2)r^2-(1)/(2)r^2 \\ \\ -10=r^2 \end{gathered}`

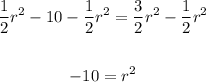
Next, take square root of both sides

`r=\pm\sqrt[]{-10}`

The solutions are:

`\begin{gathered} r=\sqrt[]{-10} \\ \\ \text{and} \\ \\ r=-\sqrt[]{-10} \end{gathered}`

There is no real solution, only imaginary.