To solve this problem we use the following formula:

Where:
p: proportion of the population
n: sample
z: This is the value given by the % of confidence and the normal distribution
First, we identify the variables of the problem:
n = 523
d = 141
alpha = (1-%confidence)/2
Second, we find the values of p and z:
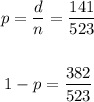
And for Z, we find the value of B such that:
/(523)\pm1.96\sqrt{(141)/(523)\cdot(382)/(523)(1)/(523)}]()
As result, we get that:
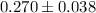
And the inferior limit is equal to 0.232 and the superior limit is equal to 0.308