Let's divide equation 1 into two groups.
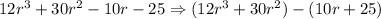
We now have two groups and these are (12r³ + 30r²) and (10r + 25).
For the first group, factor out 6r². It becomes 6r²(2r + 5).
For the second group, factor out 5. It becomes 5(2r + 5).
So, the entire equation can be written as:
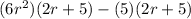
As we can see above, 2r - 5 is a common term on both groups, hence, we can rewrite the equation again as:

Since 6r² - 5 cannot be factored further, the factors of equation 1 are (2r + 5)(6r² - 5).