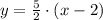Question

Write the equation in both slope-intercept form and point slope form

Answer 1

The slope-intercept equation is:

`y=m\cdot x+b,`

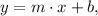
where m is the slope and b is the value of the y-intercept.

The point-slope equation is:

`y=m\cdot(x-x_0)+y_0,`

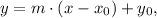
where m is the slope and (x0,y0) are the coordinates of one point of the line.

From the graph of the line, we see that it passes through the points:

• (x0,y0) = (2,0),

,

• (x1,y1) = (0,-5).

The slope of the line is given by:

`m=(y_1-y_0)/(x_1-x_0)=(-5-0)/(0-2)=(5)/(2)\text{.}`

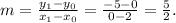
The value of the y-intercept b is the value of y when x = 0, so in this case, we have:

`b=-5.`

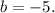
Replacing the values obtained of m, b and (x0,y0) in the equations above, we find that:

• The, slope-intercept, equation is:

`y=(5)/(2)\cdot x-5`

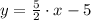
• The ,point-slope, equation is:

`y=(5)/(2)\cdot(x-2)`