Question

The elongation E of a spring balance varies directly with the applied weight W. If E =5 when W=25, find E when W=20

Answer 1

This is a question on variation. Our approach is to make equations of the various statements.

`\begin{gathered} \text{The elongation, E varies directly with weight, W can be given as:} \\ E\alpha W \end{gathered}`

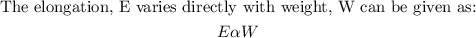
Introducing our proportionality constant, we have:

`\begin{gathered} E=kW \\ k=(E)/(W) \\ \text{where k is length per weight} \\ k=(5)/(25)=(1)/(5) \end{gathered}`

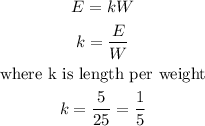
Now, we apply this constant to find the value of E given W or W, given E.

Here, we are given W and are asked to find E.

`\begin{gathered} E=kW \\ k=(1)/(5) \\ W=20 \\ E=(1)/(5)*20=4 \end{gathered}`

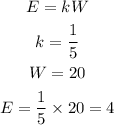
E = 4