Question

Find the slope of a line crossing through the following points (-8,14) and (6,20) answer in a simplified fraction if necessary

Answer 1

Step 1. The two points that cross through the line are:

`\begin{gathered} (-8,14) \\ (6,20) \end{gathered}`

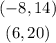
And we are required to find the slope as a simplified fraction.

Step 2. For reference, we will label the points as (x1,y1) and (x2,y2):

`(-8,14)\rightarrow x_1=-8,\text{ }y_1=14`
`(6,20)\rightarrow x_2=6,\text{ }y_2=20`

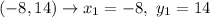
Step 3. To find the slope 'm' we use the slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

Substituting the known values:

`m=(20-14)/(6-(-8))`

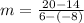
Step 4. Solving the operations:

`\begin{gathered} m=(6)/(6+8) \\ m=(6)/(14) \end{gathered}`

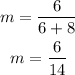
Simplifying the fraction by dividing both numbers by 2:

`m=(6)/(14)=\boxed{(3)/(7)}`

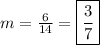
The slope is 3/7.

Answer:

`(3)/(7)`