Question

Hello, I need some assistance with this precalculus homework question, please?HW Q7

Answer 1

The correct answer is option A. The solution is ( 2, 2, -1 )

Step-by-step explanation:

First, let's write the system as a matrix:

`\begin{bmatrix}{1} & {1} & {-1} & |{\text{ }5} \\ {2} & {-3} & {8} & |{-10} \\ 1{} & {3} & {-4} & {|\text{ }12} \\ {} & {} & {} & {}\end{bmatrix}`

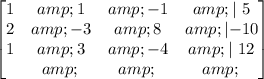
Now, we can apply rows operations. Our first objective is to only let a 1 at the top of column 1, and the rest of the column zeros.

Then, we can rest 2 times the first row to the second one; and rest once the first row to the third.

The resulting rows are:

`\begin{gathered} Resulting\text{ }2º\text{ }row: \\ (2,-3,8,-10)-2(1,1,-1,5)=(2,-3,8,-10)-(2,2,-2,10)=(0,-5,10,-20) \end{gathered}`
`\begin{gathered} Resulting\text{ }3º\text{ }row: \\ (1,3,-4,12)-(1,1,-1,5)=(0,2,-3,7) \end{gathered}`

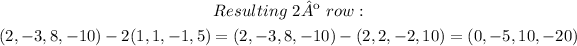
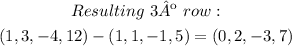
The matrix is now:

`\begin{bmatrix}{1} & {1} & {-1} & |{\text{ }5} \\ {0} & -5 & 10 & |-20 \\ 0{} & 2 & {-3} & {|\text{ 7}} \\ & & & \end{bmatrix}`

Next, we want the first number in the second row to be a 1. Then, we can divide the second row by (-5):

`\begin{gathered} Resulting\text{ }2º\text{ }row: \\ -(1)/(5)(0,-5,10,-20)=(0,1,-2,4) \end{gathered}`

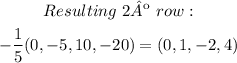
The matrix is now:

`\begin{bmatrix}{1} & {1} & {-1} & |{\text{ }5} \\ {0} & 1 & -2 & |4 \\ 0{} & 2 & {-3} & {|\text{ 7}} \\ & & & \end{bmatrix}`

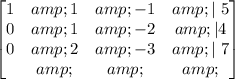
Now, we want to eliminate the numbers above and below the 1 in the second row. Then, we can rest the second row to the first one, and rest twice the 2º row to the 3º one:

`\begin{gathered} Resulting\text{ }1º\text{ }row: \\ (1,1,-1,5)-(0,1,-2,4)=(1,0,1,1) \end{gathered}`

`\begin{gathered} Resulting\text{ }3º\text{ }row: \\ (0,2,-3,7)-2(0,1,-2,4)=(0,2,-3,7)-(0,2,-4,8)=(0,0,1,-1) \end{gathered}`

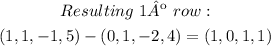
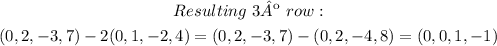
The matrix now is

`\begin{bmatrix}{1} & {0} & 1 & |1 \\ {0} & 1 & -2 & |4 \\ 0{} & 0 & 1 & |-1 \\ & & & \end{bmatrix}`

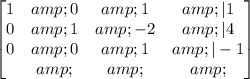
Finally, we want to eliminate all the 1's above the 1 in the 3º row.

We can rest the 3º row to the 1º. Add twice the 3º row to the 2º one:

`\begin{gathered} Resulting\text{ }1º\text{ }row: \\ (1,0,1,1)-(0,0,1,-1)=(1,0,0,2) \end{gathered}`
`\begin{gathered} Result\imaginaryI ng\text{ }2º\text{ }row: \\ (0,1,2,4)-2(0,0,1,-1)=(0,1,2,4)-(0,0,2,-2)=(0,1,0,2) \end{gathered}`

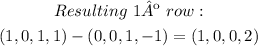
The solved matrix is:

`\begin{bmatrix}{1} & {0} & 0 & |2 \\ {0} & 1 & 0 & |2 \\ 0{} & 0 & 1 & |-1 \\ & & & \end{bmatrix}`

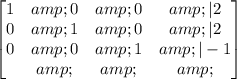
Thus:

`\begin{gathered} x=2 \\ y=2 \\ z=-1 \end{gathered}`

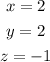
We can also check that this is a solution by verifying the initial equations:

`\begin{gathered} 2+2-(-1)=5 \\ 2\cdot2-3\cdot2+8(-1)=4-6-8=-10 \\ 2+3\cdot2-4(-1)=2+6+4=12 \end{gathered}`

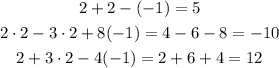
All the values works in the equation system, then the solution is (2, 2, -1)