Question

Look at the picture below. What is the probability of randomly choosing a chocolate chewy, not replacing it, and then choosing a gumball?2/95/213/2715/29

Answer 1

The picture represents 10 gumballs, and 5 chocolate chewy.

Consider that the probability of an event is given by,

`\text{Probability}=\frac{\text{ No. of favorable outcomes}}{\text{Total no. of outcomes}}`

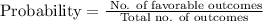
The probability of choosing a chocolate chewy and then a gumball withou replacement, is calculated as,

`\begin{gathered} P(\text{ chocolate chewy then gumball)}=\frac{\text{ No. of chocolate chewy}}{\text{Total number of items}}*\frac{\text{ No. of gumballs}}{\text{Total no. of items left}} \\ P(\text{chocolate chewy then gumball)}=(5)/(15)*(10)/(14) \\ P(\text{chocolate chewy then gumball)}=(5)/(21) \end{gathered}`

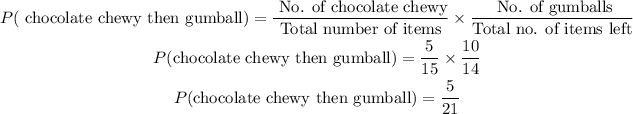
Thus, the required probability is 5/21 .