We have to approximate the area under the curve using the given rectangles.
Each rectangle will have an area that is equal to the width (the interval Δx) times the height (that is f(xi)).
We can express the formula for the approximation as:

We will have to calculate f(x) for x = 0, 4, 8 and 12, which are the left endpoints of the interval for each rectangle.
Given that f(x) is defined as:
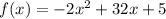
we can calculate each value as:

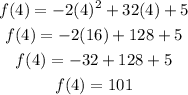
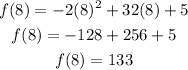

We can now calculate the approximation as:
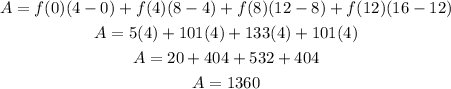
Answer: the approximation is equal to 1360 square units [Fourth option].