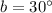Question

I need help in this it would be of great help

Answer 1

The measure of angle b is;

`b=30^(\circ)`

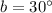
Step-by-step explanation:

Given the figure in the attached image.

line m and n are parallel lines.

To solve for angle b, let x represent the corresponding angle to angle 120 degree, as shown below;

So, angle x is equal to 120 degree.

`x=120^(\circ)`

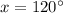
Reason: corresponding angle.

Angle x is an exterior angle to the triangle alog the line n.

So, angle x equals the sum of angle b and 90 degree.

`\begin{gathered} x=b+90^(\circ) \\ b=x-90^(\circ) \end{gathered}`

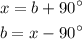
Reason: Exterior angle theorem of a triangle.

substituting the value of x;

`\begin{gathered} b=x-90^(\circ) \\ b=120^(\circ)-90^(\circ) \\ b=30^(\circ) \end{gathered}`

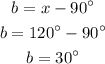
Therefore, the measure of angle b is;

`b=30^(\circ)`