Given:
The mass of the raft is m = 25 kg
The coefficient of kinetic friction is

The displacement from the ground is d = 14 m
The power of the motor is

The velocity is constant.
Required: Time required by raft to reach the top deck.
Step-by-step explanation:
First, we need to calculate the applied force.
Since the velocity is constant,
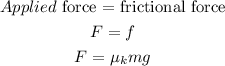
Here, g = 9.8 m/s^2 is the acceleration due to gravity.
On substituting the values, the applied force will be
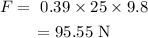
Now, the work done can be calculated as

Thus, the time can be calculated as
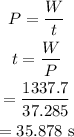
Final Answer: The raft takes 35.878 s to reach the top deck.