Question

what is the intersection point of the lines y=6x+7 and y=-9x-2? are these linear or quadratic equations

Answer 1

In general, the slope-intercept form of a linear equation is

`y=mx+b`

where m and b are constants.

Therefore, both y=6x+7 and y=-9x-2 are linear equations.

To find the intersection point, solve the system that consists of the two above linear equations

`\begin{cases}y=6x+7 \\ y=-9x-2\end{cases}`

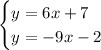
Then,

`\begin{gathered} y=y \\ \Rightarrow6x+7=-9x-2 \\ \Rightarrow15x=-9 \\ \Rightarrow x=-(9)/(15)=-(3)/(5) \\ \Rightarrow x=-(3)/(5) \end{gathered}`

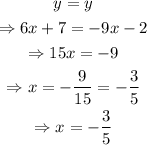
Substitute the value of x into the first equation, as shown below,

`\begin{gathered} x=-(3)/(5) \\ \Rightarrow y=6(-(3)/(5))+7=-(18)/(5)+(35)/(5)=(17)/(5) \\ \Rightarrow y=(17)/(5) \end{gathered}`

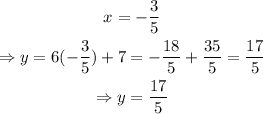
Thus, the intersection point is (-3/5,17/5)=(-0.6,3.4)