Question

15For each ordered pair, determine whether it is a solution to the system of equations.9x-2y=8-7x+3y=1(x, y)(-8, 1)(2,5)(0, -4)(-4,-9)Is it a solution?YesNoinaya ATCholticetnl 265 madaye T

Answer 1

To know if a pair of numbers x,y satisfies the given system of equations we have to replace each given pair of numbers and look ifthe equation is fulfilled.

Let's start with the pair -8,1:

`\begin{gathered} 9x-2y=8 \\ 9\left(-8\right)-2\left(1\right)=-74 \\ \end{gathered}`

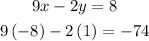
Because -74 is different from 8, the first pair of number is not a solution.

Now the second pair 2,5:

`\begin{gathered} 9x-2y=8 \\ 9(2)-2(5)=8 \\ -7x+3y=1 \\ -7(2)+3(5)=1 \end{gathered}`

Hence the second pair of number is a solution.

Let's continue with 0.-4:

`\begin{gathered} 9x-2y=8 \\ 9(0)-2(4)=-8 \\ -7x+3y=1 \\ -7*0+3(-4)=-12 \end{gathered}`

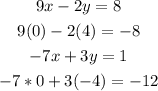
Despite it satisfies the first equation, the second one is not fulfilled. Hence the third option is not a solution.

Finally let's check -4,-9:

`\begin{gathered} 9x-2y=8 \\ 9(-4)-2(-9)=-18 \end{gathered}`

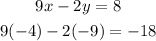
Then the last option is not a solition.

The answer then is: No, Yes, No, No.