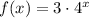Question

write an equation for the exponential function that includes the pair of given points. (1, 12) and (-1, 0.75)

Answer 1

Given the points (1, 12) and (-1, 0.75)

We will write the exponential function that includes the given points

Let the expression of the function will be as follows:

`f(x)=a\cdot b^x`

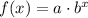
When x = 1, f = 12

so,

`12=a\cdot b\rightarrow(1)`

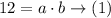
When x = -1, f = 0.75

So,

`\begin{gathered} 0.75=a\cdot b^(-1) \\ 0.75=(a)/(b)\rightarrow(2) \end{gathered}`

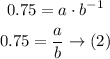
Solve the equations (1) and (2) to find (a) and (b)

Multiply the equations to eliminate (b)

`\begin{gathered} 12\cdot0.75=a^2 \\ a^2=9 \\ a=\sqrt[]{9}=3 \end{gathered}`

Substitute with (a) into equation (1) to find (b)

`\begin{gathered} 12=3b \\ b=(12)/(3)=4 \end{gathered}`

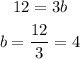
So, the answer will be:

The equation of the exponential function will be as follows:

`f(x)=3\cdot4^x`