Let's call x the pure antifreeze in gallons. This means 4 + x represents the new quantity of pure antifreeze.
According to the problem, 25% of the solution represents 4 gallons and 50% of the solution represents the new quantity of antifreeze.
Based on the given information, we can express the following.
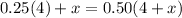
Let's solve for x.
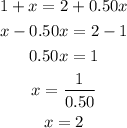
Therefore, he needs to add 2 gallons of pure antifreeze.