Given:
The geometric sequence
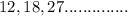
Find-:
The sum of the first 8 terms of the geometric sequence
Explanation-:
The sum of a geometric sequence is:
Where,

The geometric sequence is:
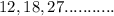
The common ratio is:
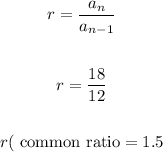
Sum of the first 8 terms is:
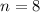
So, the sum of the first 8 terms is:
r is greater than 1, so the formula is:

The sum of the first 8 terms is 591.09