Question

Suppose a sample of 726 suspected criminals is drawn. Of these people, 232 were captured. Using the data, estimate the proportion of people who were caught after being on the 10 most wanted list. Enter your answer as a fraction or decimal number rounded to three decimal places.

Answer 1

Step-by-step explanation

Algebra / Rational Expressions / Percent / Proportions and Percents

From the statement, we know that:

• a sample of 726 suspected criminals is drawn,

,

• and from these people, 232 were captured.

Part 1

We have to estimate the proportion of people who were caught. We compute the quotient between 232 and 726, and we get:

`p=(232)/(726)\cong0.3195592\cong0.320.`

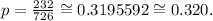
Part 2

We must construct the 98% confidence interval for the population proportion p.

1) First, we compute the coefficient α of the confidence interval:

`\begin{gathered} α=1-98\%=1-0.98=0.02, \\ α/2=0.02/2=0.01. \end{gathered}`

2) From a table of z-scores, the z-score for α/2 is:

`Z_(α/2)=Z_(0.01)=2.326.`

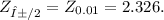
3) The margin of error ε of the confidence interval p - ε < p < p + ε, is given by:

`ε=Z_(α/2)\cdot\sqrt{(p\cdot(1-p))/(n)}`

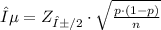
Where n = 726 is the size of the sample.

Replacing the data obtained in the previous steps, we get:

`ε=2.326\cdot\sqrt{((232)/(726)\cdot(1-(232)/(726)))/(726)}\cong0.040254\cong0.04.`

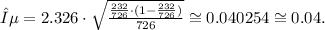
The confidence interval is:

[tex]\begin{gathered} p-ε

The lower limit of the 98% confidence interval is 0.316.

Answer

Part 1

• As a fraction: ,232/726

,

• In decimal form: ,0.320

Part 2

• Lower endpoint: ,0.316

,

• Upper endpoint: ,0.324