Question

I need help with the attached problem and the solution has the following suffix as options: feetfeet^2, feet ^3

Answer 1

The area of the border is equal to

`A=(32+2x)(20+2x)-(32)(20)`

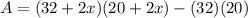
Expand the equation

`\begin{gathered} A=640+64x+40x+4x^2-640 \\ A=4x^2+104x \end{gathered}`

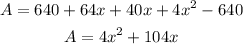
Remember that the area of the border is given

A=224 ft2

substitute and solve the quadratic equation

`\begin{gathered} 4x^2+104x=224 \\ 4x^2+104x-224=0 \end{gathered}`

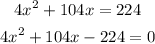
using the formula

a=4

b=104

c=-224

substitute

`x=(-104\pm√(104^2-4(4)(-224)))/(2(4))`
`x=(-104\pm120)/(8)`

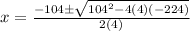
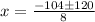
The values of x are

x=2 ft and x=-28 ft ( is not a solution because is a negative number)

therefore

The answer is 2 ft