Question

Systems of Equations1) Create a real-world problem involving a related set of two equations.2) Write the system of equations that would be used to solve them.3) Show how to solve the same system using ALL 3 methods:• Graphing, Substitution, Elimination4) Identify your solution & explain what it means in the context of your word problem!

Answer 1

1) Create a real-world problem involving a related set of two equations

George bought 5 apples and 2 peaches, he pays $22.00. Isabella bought 10 apples and 2 peaches, she pays $32.00. a) How much does an apple cost? b) How much does a peach cost?

2)Write the system of equations that would be used to solve them.

Let x be the cost of an apple

Let y be the cost of a peach

George bought 5 apples and 2 peaches, he pays $22.00:

`5x+2y=22`

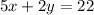
Isabella bought 10 apples and 2 peaches, she pays $32.00:

`10x+2y=32`

System of equations:

`\begin{gathered} 5x+2y=22 \\ 10x+2y=32 \end{gathered}`

3) Show how to solve the same system using ALL 3 methods:

• Graphing

Find two points (x,y) for each equation:

-First equation:

`\begin{gathered} When\text{ }x=0 \\ 5(0)+2y=22 \\ 2y=22 \\ y=(22)/(2) \\ y=11 \\ Point(0,11) \\ \\ When\text{ }x=6 \\ 5(6)+2y=22 \\ 30+2y=22 \\ 2y=22-30 \\ 2y=-8 \\ y=-(8)/(2) \\ y=-4 \\ Point(6,-4) \end{gathered}`

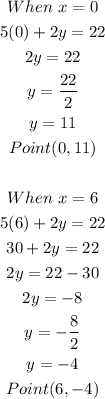
-Second equation:

`\begin{gathered} When\text{ }x=0 \\ 10(0)+2y=32 \\ 2y=32 \\ y=(32)/(2) \\ y=16 \\ Point(0,16) \\ \\ When\text{ }x=4 \\ 10(4)+2y=32 \\ 40+2y=32 \\ 2y=32-40 \\ 2y=-8 \\ y=-(8)/(2) \\ y=-4 \\ Point(4,-4) \end{gathered}`

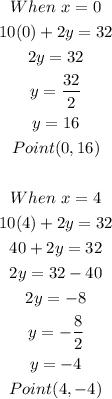
Use each pair of points to graph the corresponding line: Put the point in the plane and draw a line that passes through the corresponding pair of points:

The solution is the point of intersection (2,6)

• Substitution:

`\begin{gathered} 5x+2y=22 \\ 10x+2y=32 \end{gathered}`

1. Solve x in the first equation:

`\begin{gathered} 5x+2y=22 \\ 5x=22-2y \\ x=(22)/(5)-(2)/(5)y \end{gathered}`

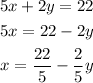
2. Substitute x in the second equation with the value you get in the first step:

`10((22)/(5)-(2)/(5)y)+2y=32`

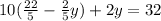
3. Solve y:

`\begin{gathered} (220)/(5)-(20)/(5)y+2y=32 \\ \\ 44-4y+2y=32 \\ \\ 44-2y=32 \\ \\ -2y=32-44 \\ \\ -2y=-12 \\ \\ y=(-12)/(-2) \\ \\ y=6 \end{gathered}`

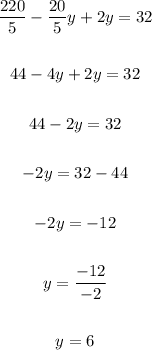
4. Use the value of y to solve x:

`\begin{gathered} x=(22)/(5)-(2y)/(5) \\ \\ x=(22)/(5)-(2(6))/(5) \\ \\ x=(22)/(5)-(12)/(5) \\ \\ x=(22-12)/(5) \\ \\ x=(10)/(5) \\ \\ x=2 \end{gathered}`

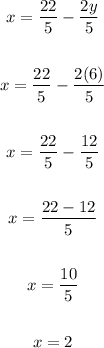
The solution is (2,6)

• Elimination:

`\begin{gathered} 5x+2y=22 \\ 10x+2y=32 \end{gathered}`

1. Subtract the equations:

2. Solve x:

`\begin{gathered} -5x=-10 \\ x=(-10)/(-5) \\ x=2 \end{gathered}`

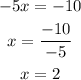
3. Use the value of x to solve y:

`\begin{gathered} 5x+2y=22 \\ 5(2)+2y=22 \\ 10+2y=22 \\ 2y=22-10 \\ 2y=12 \\ y=(12)/(2) \\ y=6 \end{gathered}`

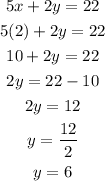
The solution is (2,6)

4) Identify your solution & explain what it means in the context of your word problem!

The solution is (2,6), x=2, y=6

The meaning of the solution is: The cost of an apple is $2.00 and the cost of a peach is $6.00